Week Three Lecture MTH 208

Linear Equations and Inequalities

Introduction

This week we extend the topic of linear equations and inequalities to multiple variables. We will also develop the concept of “function”.

More Linear Equations

As we mentioned last week, one-variable linear equations can be written in the form

Equation 1. ax + b = 0

where a and b are constants. For two variables, this can be extended to

Equation 2. ax + by + c = 0

where “x” and “y” are variables and “a”, “b”, and “c” are constants.

Like the linear equations discussed last week, the two-variable linear equations have no multiplication or division, except by constants. There are a number of applications for linear equations with more than two variables; If we keep adding variables, we can run out of letters of the alphabet. Some textbook writers number the constants and variables with subscripts:

Equation 3. a₀ + a₁x₁ + a₂x₂ + a₃x₃ ... = 0

where the a's are constants and the x's are variables. The “...” indicates that we can add as many of these constant and variable pairs as we want. Notice that a₀ is not multiplied by a variable; it corresponds to the “c” in the two-variable equation.

Other Linear Equation Formats

If we put the “c” on the right side of Equation 2, we get the what our textbook calls the "standard format"

Equation 4. ax + by = c

As our textbook points out on page 182, any straight line on the x-y plane can be written as an equation in standard format. In fact, for every straight line there are an infinite number of equations in standard format; take the first one that fits and multiply both sides by any real number except zero. With all of these “standard” equations, there must be a basis for selecting one of them.

Equation 5a. ax + y = c if b ≠ 0
Equation 5b. x = c if b = 0

The format of equation 5a can easily be modified to make y a function of x (more about functions later). If the constant “b” in the standard format is zero, the line is vertical and not a function.

What is a Function

The classic definition of a function is a pairing of items in the two sets called the domain and the range:

for every member of the domain, d, there is a single corresponding member of the range, r, such that f(d) = r

The range and domain need not be numbers. The domain could be the students in this class and the range could be the state or province of residence. Two members of the domain could be paired with the same range member. The reverse is not true; if even one member of the domain can be paired with two members of the range, the relation is not a function. Shoe size is not a function, since some people have different sized feet.

In the Cartesian coordinate system (x, y grid) y is sometimes used as a synonym for a function of x. You may see “y = 3x – 2” and “f(x) = 3x – 2” used interchangeably.

In computer programming, the concept of “function” was copied from the language of mathematics. In Fortran, functions received input (corresponding to members of the domain) and returned a single result. Excel spreadsheets inherited most of the Fortran built-in functions and added many new ones. When you bring up the formula wizard in excel, you see a huge selection of functions, some (like cosine) for which the input is a single cell and others (such as sum) for which the input is a group of cells. Programming languages (including excel) let the users write their own functions.

Line Through Two Points

As you may remember from geometry, "two points determine a line". In other words, if we have two points, (x₁, y₁) and (x₂, y₂), we can plot a straight line that goes through both of them. Suppose the two points are at (1, 4) and (3, 8). Since the line is not vertical (the two values of x are different) we can plug the points into equation 5a and solve for the constant “a”.

1a + 4 = 3a + 8 now subtract 8 from both sides
1a -4 = 3a now subtract a from both sides and divide by 2
-2 = a
Now we are ready to calculate the value of c, since we know that a=-2 and b=1.

Using the first point (x=1, y=4) we get c = -2x + 4 = 2, so the formula for the line between these two points is -2x + y = 2. If you plug in the x's and y's from the two points, you find that they both check.

This method, solving for a and using the result to solve for c, produces the same result as our textbook shows on page 191. I describe the method that I first learned because it is the one I'm most familiar with. Feel free to use the method that you find easier.

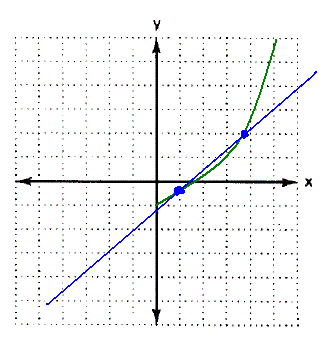
Linear Interpolation

Now that we can determine the equation for a line given two points, you may wonder what it is used for.

One use involves unknown functions. Fortunately for our calculations, most functions can be approximated by a series of line segments. If we take measurements at two points, we can connect them on a graph with a straight line. Usually, the line will be close to the actual value between the two points and diverge to the sides.

One example of the use of linear interpolation is water pressure in a lake. If we measure the pressure at 10 feet and at 20 feet, we can use a straight line graph to estimate the pressures between these depths. If we extend the line below 50 feet deep, it will become inaccurate because cool, denser water sinks to the bottom of the lake. If we extend the graph upward, it would become very inaccuaate because air is much less dense than water.

Linear Inequalities

If we have a straight line, represented by “y = ax + b”, then “y > ax + b” is the region above the line and “y <ax + b” is the region below the line. If the line is vertical, the two regions will be on the right and on the left.

By themselves, linear inequalities handle the comparisons between two unknowns. Next week, we will see how they can be combined to produce single solutions.

A Note on Text Formatting

You use subscripts for things in a series. If it makes sense to say "the first a and the second a" you could refer to them as "a₁ and a₂".

One way to get the subscripts is to use the "source" button at the bottom of the Outlook Express (OE) composition box. This lets you enter the HTML for subscripting "R1 and R2". If you don't see this tab, go to the View pull-down menu and make sure that the "source edit" option is checked.

You can get exponents into your messages, a similar manner. "R1 and R2" becomes "R¹ and R²". An easier way to include the second ant third power is to hold down the “ALT” key while typing on the numeric keypad on the right side of the keyboard. ALT-0178 gives “²” and ALT-0179 gives “³”.

Graphs with Excel

Cartesian graphs have become a standard illustration in newspapers, almost as common as photographs. One reason for the increase in their use is automated graphing. Not too long ago, the only way to plot a graph involved a pencil and graph paper. With the introduction of graphic spreadsheets, the "chart wizard" takes over this process.

All that you need to do is place the x and y coordinates, side by side, in the spreadsheet, highlight the data, click the chart wizard icon, and follow the directions. The chart type for the graphs covered in our textbook is called "xy scatter" and the subtype is "scatter with data points connected by lines".

Discussion Questions

Here is an exercise in linear interpolation on the curve y=x². Estimate the value at x=17.5 by drawing a straight line between (15, 15²) and (20,20²); now try a line between (17, 17²) and (18, 18²); finally try (17.4, 17.4²) and (17.6, 17.6²). How does the accuracy of the estimate improve as the line segment gets shorter?
Can you think of a function for which linear interpolation would not provide a reasonable approximation?
How would you graph a linear equation in three variables? What would it look like?
How would you answer question 52 on page 444?